Nomor 11
Diketahui $f(x) = ax^2+bx+4 $ . Jika gradien garis singgung kurva di $ x = 2 \, $ adalah $-1 \, $ dan di $ x = 1 \, $ adalah 3,
maka $ a+b = .... $
$\spadesuit \, $ Konsep Dasar Gradien ($m$) garis singgung : $ m = f^\prime (x) $
$f(x) = ax^2+bx+4 \rightarrow f^\prime (x) = 2ax + b $
$\spadesuit \, $ Substitusi semua gradiennya dengan $ \, f^\prime (x) = 2ax + b $
* $ m = -1 \, \, $ saat $ \, x = 2 \, \, $ substitusi ke $ \, m = f^\prime (x) $
$ \, \, \, -1 = f^\prime (2) \rightarrow -1 = 2a.2 + b \rightarrow 4a + b = -1 \, \, $ ...pers(i)
* $ m = 3 \, \, $ saat $ \, x = 1 \, \, $ substitusi ke $ \, m = f^\prime (x) $
$ \, \, \, 3 = f^\prime (1) \rightarrow 3 = 2a.1 + b \rightarrow 2a + b = 3 \, \, $ ...pers(ii)
$\spadesuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} 4a + b = -1 & \\ 2a + b = 3 & - \\ \hline 2a=-4 & \\ a = -2 & \end{array} $
pers(ii) : $ 2a + b = 3 \rightarrow 2.(-2) + b = 3 \rightarrow b = 7 $
Sehingga : $a+b = -2 + 7 = 5 $
Jadi, nilai $ a + b = 5. \heartsuit $
$f(x) = ax^2+bx+4 \rightarrow f^\prime (x) = 2ax + b $
$\spadesuit \, $ Substitusi semua gradiennya dengan $ \, f^\prime (x) = 2ax + b $
* $ m = -1 \, \, $ saat $ \, x = 2 \, \, $ substitusi ke $ \, m = f^\prime (x) $
$ \, \, \, -1 = f^\prime (2) \rightarrow -1 = 2a.2 + b \rightarrow 4a + b = -1 \, \, $ ...pers(i)
* $ m = 3 \, \, $ saat $ \, x = 1 \, \, $ substitusi ke $ \, m = f^\prime (x) $
$ \, \, \, 3 = f^\prime (1) \rightarrow 3 = 2a.1 + b \rightarrow 2a + b = 3 \, \, $ ...pers(ii)
$\spadesuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} 4a + b = -1 & \\ 2a + b = 3 & - \\ \hline 2a=-4 & \\ a = -2 & \end{array} $
pers(ii) : $ 2a + b = 3 \rightarrow 2.(-2) + b = 3 \rightarrow b = 7 $
Sehingga : $a+b = -2 + 7 = 5 $
Jadi, nilai $ a + b = 5. \heartsuit $
Nomor 12
Jika $ f(x) = \frac{1}{\sqrt{x}} $ , maka $ -2f^\prime (x) = .... $
$\clubsuit \, $ Rumus dasar Turunan : $ y = x^n \rightarrow y^\prime = n x^{n-1} $
$\clubsuit \, $ Menentukan turunan fungsi
$\begin{align} f(x) & = \frac{1}{\sqrt{x}} \\ f(x) & = x^\frac{-1}{2} \\ f^\prime (x) & = \frac{-1}{2}x^{\frac{-1}{2} - 1 } = -\frac{1}{2}x^\frac{-3}{2} = -\frac{1}{2} \frac{1}{x^\frac{3}{2}} \\ f^\prime (x) & = -\frac{1}{2} \frac{1}{x\sqrt{x}} \end{align}$
Sehingga : $ -2f^\prime (x) = -2 . -\frac{1}{2} \frac{1}{x\sqrt{x}} = \frac{1}{x\sqrt{x}} $
Jadi, nilai $ -2f^\prime (x) = \frac{1}{x\sqrt{x}} . \heartsuit $
$\clubsuit \, $ Menentukan turunan fungsi
$\begin{align} f(x) & = \frac{1}{\sqrt{x}} \\ f(x) & = x^\frac{-1}{2} \\ f^\prime (x) & = \frac{-1}{2}x^{\frac{-1}{2} - 1 } = -\frac{1}{2}x^\frac{-3}{2} = -\frac{1}{2} \frac{1}{x^\frac{3}{2}} \\ f^\prime (x) & = -\frac{1}{2} \frac{1}{x\sqrt{x}} \end{align}$
Sehingga : $ -2f^\prime (x) = -2 . -\frac{1}{2} \frac{1}{x\sqrt{x}} = \frac{1}{x\sqrt{x}} $
Jadi, nilai $ -2f^\prime (x) = \frac{1}{x\sqrt{x}} . \heartsuit $
Nomor 13
Nilai - nilai yang memenuhi pertaksamaan $ \, \frac{2x-1}{3x+2} \geq 2 \, $ adalah ....
$\spadesuit \, $ Menyelesaikan pertidaksamaan
$\begin{align*} \frac{2x-1}{3x+2} & \geq 2 \\ \frac{2x-1}{3x+2} -2 & \geq 0 \\ \frac{2x-1}{3x+2} - \frac{2(3x+2)}{3x+2} & \geq 0 \\ \frac{-4x-5}{3x+2} & \geq 0 \\ x = -\frac{5}{4} \, & \vee \, x = -\frac{2}{3} \end{align*}$
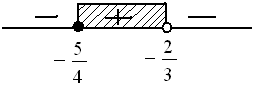
Catatan : Akar - akar penyebut tidak diikutkan (pasti bolong)
Jadi, solusinya adalah $ HP = \{ -\frac{5}{4} \leq x < -\frac{2}{3} \} . \heartsuit $
$\begin{align*} \frac{2x-1}{3x+2} & \geq 2 \\ \frac{2x-1}{3x+2} -2 & \geq 0 \\ \frac{2x-1}{3x+2} - \frac{2(3x+2)}{3x+2} & \geq 0 \\ \frac{-4x-5}{3x+2} & \geq 0 \\ x = -\frac{5}{4} \, & \vee \, x = -\frac{2}{3} \end{align*}$

Catatan : Akar - akar penyebut tidak diikutkan (pasti bolong)
Jadi, solusinya adalah $ HP = \{ -\frac{5}{4} \leq x < -\frac{2}{3} \} . \heartsuit $
Nomor 14
Deret $S_4 = U_1 + U_2+U_3+U_4 \, $ merupakan deret aritmetika dan $ U_1 > U_2 \, $. Jika determinan matriks
$\left( \begin{matrix} U_1 & U_2 \\ U_3 & U_4 \end{matrix} \right) \, $ adalah $ -2 \, $ dan $ S_4=2 , \, $
maka $\left( \begin{matrix} U_1 & U_2 \\ U_3 & U_4 \end{matrix} \right)^{-1} = .... $
$\clubsuit \,$ Barisan Aritmetika : $ U_n = a+ (n-1)b \, \, \, $ dan $ \, S_n = \frac{n}{2}(2a+(n-1)b) $
karena $ U_1 > U_2 \, $ , maka bedanya negatif ($b < 0 $ ) .
$\clubsuit \,$ Menentukan determinan
$\begin{align} \left| \begin{matrix} U_1 & U_2 \\ U_3 & U_4 \end{matrix} \right| & = -2 \\ U_1.U_4 - U_2.U_3 & = -2 \\ a.(a+3b) - (a+b).(a+2b) & = -2 \\ a^2+3ab - (a^2+3ab+2b^2) & = -2 \\ -2b^2 & = -2 \\ b^2 & = 1 \rightarrow b = \pm 1 \end{align}$
yang memenuhi adalah $ b = -1 \, $ karena harus negatif
$\clubsuit \,$ Menentukan nilai $ \, a $ dari $ S_4 = 2 $
$ S_4=2 \rightarrow \frac{4}{2}(2a+3b) = 2 \rightarrow 2(2a+3.(-1)) = 2 \rightarrow a = 2 $
$\clubsuit \,$ Menentukan matriksnya
$A = \left( \begin{matrix} U_1 & U_2 \\ U_3 & U_4 \end{matrix} \right) = \left( \begin{matrix} a & a+b \\ a+2b & a+3b \end{matrix} \right) $
$ A = \left( \begin{matrix} 2 & 2+(-1) \\ 2+2.(-1) & 2+3.(-1) \end{matrix} \right) = \left( \begin{matrix} 2 & 1 \\ 0 & -1 \end{matrix} \right) $
$\clubsuit \,$ Menentukan Invers matriksnya
Konsep Invers : $ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow A^{-1} = \frac{1}{ad-bc} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) $
$\begin{align} A = \left( \begin{matrix} 2 & 1 \\ 0 & -1 \end{matrix} \right) \rightarrow A^{-1} & = \frac{1}{ad-bc} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) \\ A^{-1} & = \frac{1}{(-1.2)-(0.(-1))} \left( \begin{matrix} -1 & -1 \\ 0 & 2 \end{matrix} \right) \\ & = \frac{1}{-2} \left( \begin{matrix} -1 & -1 \\ 0 & 2 \end{matrix} \right) \\ & = \left( \begin{matrix} \frac{1}{2} & \frac{1}{2} \\ 0 & -1 \end{matrix} \right) \end{align}$
Jadi, inversnya adalah $ \left( \begin{matrix} \frac{1}{2} & \frac{1}{2} \\ 0 & -1 \end{matrix} \right) . \heartsuit $
karena $ U_1 > U_2 \, $ , maka bedanya negatif ($b < 0 $ ) .
$\clubsuit \,$ Menentukan determinan
$\begin{align} \left| \begin{matrix} U_1 & U_2 \\ U_3 & U_4 \end{matrix} \right| & = -2 \\ U_1.U_4 - U_2.U_3 & = -2 \\ a.(a+3b) - (a+b).(a+2b) & = -2 \\ a^2+3ab - (a^2+3ab+2b^2) & = -2 \\ -2b^2 & = -2 \\ b^2 & = 1 \rightarrow b = \pm 1 \end{align}$
yang memenuhi adalah $ b = -1 \, $ karena harus negatif
$\clubsuit \,$ Menentukan nilai $ \, a $ dari $ S_4 = 2 $
$ S_4=2 \rightarrow \frac{4}{2}(2a+3b) = 2 \rightarrow 2(2a+3.(-1)) = 2 \rightarrow a = 2 $
$\clubsuit \,$ Menentukan matriksnya
$A = \left( \begin{matrix} U_1 & U_2 \\ U_3 & U_4 \end{matrix} \right) = \left( \begin{matrix} a & a+b \\ a+2b & a+3b \end{matrix} \right) $
$ A = \left( \begin{matrix} 2 & 2+(-1) \\ 2+2.(-1) & 2+3.(-1) \end{matrix} \right) = \left( \begin{matrix} 2 & 1 \\ 0 & -1 \end{matrix} \right) $
$\clubsuit \,$ Menentukan Invers matriksnya
Konsep Invers : $ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \rightarrow A^{-1} = \frac{1}{ad-bc} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) $
$\begin{align} A = \left( \begin{matrix} 2 & 1 \\ 0 & -1 \end{matrix} \right) \rightarrow A^{-1} & = \frac{1}{ad-bc} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) \\ A^{-1} & = \frac{1}{(-1.2)-(0.(-1))} \left( \begin{matrix} -1 & -1 \\ 0 & 2 \end{matrix} \right) \\ & = \frac{1}{-2} \left( \begin{matrix} -1 & -1 \\ 0 & 2 \end{matrix} \right) \\ & = \left( \begin{matrix} \frac{1}{2} & \frac{1}{2} \\ 0 & -1 \end{matrix} \right) \end{align}$
Jadi, inversnya adalah $ \left( \begin{matrix} \frac{1}{2} & \frac{1}{2} \\ 0 & -1 \end{matrix} \right) . \heartsuit $
Nomor 15
Panjang sisi miring suatu segitiga siku - siku adalah $ 2^{x+2} \, $ . Jika panjang dua sisi yang lain adalah 4 dan $ 2^{2x+1} \, $
, maka nilai $x \, $ yang memenuhi terletak pada interval ....
$\spadesuit \, $ Gambar
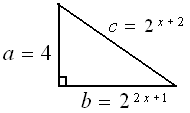
$\spadesuit \, $ Menentukan interval $x \, $ dengan $ \, c > a \, $ dan $\, c > b$
$\begin{align} c & > a \\ 2^{x+2} & > 4 \\ 2^{x+2} & > 2^2 \\ x+2 & > 2 \\ x & > 0 \, \, \, \text{...(HP1)} \end{align}$ $\begin{align} c & > b \\ 2^{x+2} & > 2^{2x+1} \\ x+2 & > 2x 1 \\ -x & > -1 \\ x & < 1 \, \, \, \text{...(HP2)} \end{align}$
Sehingga solusinya : HP = $HP_1 \cap HP_2 = \{ 0 < x < 1 \} $
Jadi, interval nilai $x \, $ adalah $ \{ 0 < x < 1 \} . \heartsuit $
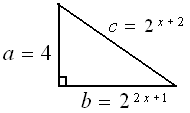
$\spadesuit \, $ Menentukan interval $x \, $ dengan $ \, c > a \, $ dan $\, c > b$
$\begin{align} c & > a \\ 2^{x+2} & > 4 \\ 2^{x+2} & > 2^2 \\ x+2 & > 2 \\ x & > 0 \, \, \, \text{...(HP1)} \end{align}$ $\begin{align} c & > b \\ 2^{x+2} & > 2^{2x+1} \\ x+2 & > 2x 1 \\ -x & > -1 \\ x & < 1 \, \, \, \text{...(HP2)} \end{align}$
Sehingga solusinya : HP = $HP_1 \cap HP_2 = \{ 0 < x < 1 \} $
Jadi, interval nilai $x \, $ adalah $ \{ 0 < x < 1 \} . \heartsuit $
Cara II :
$\spadesuit \, $ Gambar
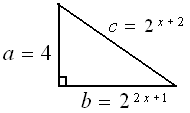
$\spadesuit \, $ Berdasarkan gambar, berlaku pythagoras yaitu :
Misalkan : $ 2^{2x} = p $
$\begin{align} a^2 + b^2 & = c^2 \\ 4^2 + (2^{2x+1})^2 & = (2^{x+2})^2 \\ 16 + 2^{4x+2} & = 2^{2x+4} \\ 16 + 2^2. 2^{4x} & = 2^4.2^{2x} \\ 16 + 4. (2^{2x})^2 & = 16.2^{2x} \, \, \, \, \, \, \text{(bagi 4)} \\ 4 + (2^{2x})^2 & = 4.2^{2x} \, \, \, \, \, \, \text{(ganti } p) \\ 4 + p^2 & = 4p \\ p^2 - 4p + 4 & = 0 \\ (p-2)^2 & = 0 \\ p & = 2 \end{align}$
nilai $ x $ :
$ p = 2 \rightarrow 2^{2x} = 2 \rightarrow 2x = 1 \rightarrow x = \frac{1}{2} $.
Sehingga nilai $ a $ ada pada interval $ \{ 0 < x < 1 \} $
Jadi, nilai $x \, $ ada pada interval $ \{ 0 < x < 1 \} . \heartsuit $
$\spadesuit \, $ Gambar
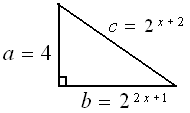
$\spadesuit \, $ Berdasarkan gambar, berlaku pythagoras yaitu :
Misalkan : $ 2^{2x} = p $
$\begin{align} a^2 + b^2 & = c^2 \\ 4^2 + (2^{2x+1})^2 & = (2^{x+2})^2 \\ 16 + 2^{4x+2} & = 2^{2x+4} \\ 16 + 2^2. 2^{4x} & = 2^4.2^{2x} \\ 16 + 4. (2^{2x})^2 & = 16.2^{2x} \, \, \, \, \, \, \text{(bagi 4)} \\ 4 + (2^{2x})^2 & = 4.2^{2x} \, \, \, \, \, \, \text{(ganti } p) \\ 4 + p^2 & = 4p \\ p^2 - 4p + 4 & = 0 \\ (p-2)^2 & = 0 \\ p & = 2 \end{align}$
nilai $ x $ :
$ p = 2 \rightarrow 2^{2x} = 2 \rightarrow 2x = 1 \rightarrow x = \frac{1}{2} $.
Sehingga nilai $ a $ ada pada interval $ \{ 0 < x < 1 \} $
Jadi, nilai $x \, $ ada pada interval $ \{ 0 < x < 1 \} . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.