Nomor 6
Banyak bilangan ratusan dengan angka pertama dan terakhir mempunyai selisih 3 adalah ...
$\spadesuit \, $ Ada beberapa kemungkinan agar angka pertama dan ketiga selisihnya 3 :
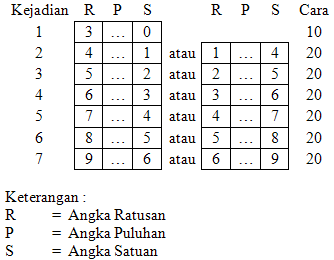
Total = 10 + 6 $\times \, $ 20 = 130 bilangan.
$\spadesuit \, $ Penjelasan:
kejadian 2, angka ratusannya angka 4 dan satuannya harus 1 (agar selisihnya 3), sementara untuk angka puluhannya bebas yang bisa dipilih dari angka 0,1, 2, 3, 4, 5, 6, 7, 8, dan 9 yaitu 10 pililihan (cara). Jika dibalik juga berlaku, ratusannya angka 1 dan satuannya harus 4 dengan banyak cara 10 pilihan untuk puluhannya. sehingga total kejadian 2 ada 10 + 10 = 20 cara. Begitu juga untuk kejadian lainnya. Sementara kejadian 1 tidak bisa dibalik karena angka ratusan tidak boleh nol (angka 0). Contoh kejadian 2 :
401, 411, 421, 431, 441, 451, 461, 471, 481, 491, dan kebalikkannya :
104, 114, 124, 134, 144, 154, 164, 174, 184, 194.
Jadi, banyak bilangan ada 130 bilangan. $ \heartsuit $

Total = 10 + 6 $\times \, $ 20 = 130 bilangan.
$\spadesuit \, $ Penjelasan:
kejadian 2, angka ratusannya angka 4 dan satuannya harus 1 (agar selisihnya 3), sementara untuk angka puluhannya bebas yang bisa dipilih dari angka 0,1, 2, 3, 4, 5, 6, 7, 8, dan 9 yaitu 10 pililihan (cara). Jika dibalik juga berlaku, ratusannya angka 1 dan satuannya harus 4 dengan banyak cara 10 pilihan untuk puluhannya. sehingga total kejadian 2 ada 10 + 10 = 20 cara. Begitu juga untuk kejadian lainnya. Sementara kejadian 1 tidak bisa dibalik karena angka ratusan tidak boleh nol (angka 0). Contoh kejadian 2 :
401, 411, 421, 431, 441, 451, 461, 471, 481, 491, dan kebalikkannya :
104, 114, 124, 134, 144, 154, 164, 174, 184, 194.
Jadi, banyak bilangan ada 130 bilangan. $ \heartsuit $
Nomor 7
Transformasi $T$ merupakan komposisi pencerminan terhadap garis $y=5x$ dilanjutkan pencerminan terhadap garis $y=-\frac{x}{5}$ .
Matriks penyajian $T$ adalah ...
$\clubsuit \, $ Menentukan gradien masing-masing garis :
$y=5x \Rightarrow m_1 = 5 \, $ dan $ \, y=-\frac{x}{5} \Rightarrow m_2 = -\frac{1}{5}$ .
$m_1.m_2 = 5. -\frac{1}{5} = -1 $ , karena perkalian gradien kedua garis nilainya -1, artinya kedua garis tegak lurus (sudutnya 90$^o$).
$\clubsuit \, $ Matriks Transformasi (MT) dua garis :
$MT = \left( \begin{matrix} \cos 2\theta & -\sin 2\theta \\ \sin 2\theta & \cos 2\theta \end{matrix} \right) $
dengan $\theta \, $ adalah sudut antara kedua garis.
Sehingga MT kedua garis :
$MT = \left( \begin{matrix} \cos 2. 90^o & -\sin 2. 90^o \\ \sin 2. 90^o & \cos 2. 90^o \end{matrix} \right) = \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right)$
Jadi, Matriks transformasinya adalah $\left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right). \heartsuit$
$y=5x \Rightarrow m_1 = 5 \, $ dan $ \, y=-\frac{x}{5} \Rightarrow m_2 = -\frac{1}{5}$ .
$m_1.m_2 = 5. -\frac{1}{5} = -1 $ , karena perkalian gradien kedua garis nilainya -1, artinya kedua garis tegak lurus (sudutnya 90$^o$).
$\clubsuit \, $ Matriks Transformasi (MT) dua garis :
$MT = \left( \begin{matrix} \cos 2\theta & -\sin 2\theta \\ \sin 2\theta & \cos 2\theta \end{matrix} \right) $
dengan $\theta \, $ adalah sudut antara kedua garis.
Sehingga MT kedua garis :
$MT = \left( \begin{matrix} \cos 2. 90^o & -\sin 2. 90^o \\ \sin 2. 90^o & \cos 2. 90^o \end{matrix} \right) = \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right)$
Jadi, Matriks transformasinya adalah $\left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right). \heartsuit$
Nomor 8
$\int 8\sin ^2 x \cos ^2 x dx = ...$
$\spadesuit \, $ Rumus dasar :
$\sin px . \cos px = \frac{1}{2}.\sin 2px \, $ dan $\sin ^2 px = \frac{1}{2}(1-\cos 2px)$ .
$\int \cos ax dx = \frac{1}{a} \sin ax + c$
$\spadesuit \, $ Menyederhanakan bentuk $\sin ^2 x \cos ^2 x$ :
$\begin{align*} \sin ^2 x \cos ^2 x & = (\sin x . \cos x)^2 \\ & = \left( \frac{1}{2}\sin 2x \right)^2 \\ & = \frac{1}{4} \sin ^2 2x \\ & = \frac{1}{4} \left[ \frac{1}{2}(1-\cos 4x) \right] \\ & = \frac{1}{8} (1-\cos 4x) \end{align*}$
$\spadesuit \, $ Menentukan hasil integral :
$\begin{align*} \int 8\sin ^2 x \cos ^2 x dx & = \int 8.\frac{1}{8} (1-\cos 4x) dx \\ & = \int (1 - \cos 4x )dx \\ & = x - \frac{1}{4}\sin 4x + c \end{align*}$
Jadi, hasil $\int 8\sin ^2 x \cos ^2 x dx = x - \frac{1}{4}\sin 4x + c. \heartsuit$
$\sin px . \cos px = \frac{1}{2}.\sin 2px \, $ dan $\sin ^2 px = \frac{1}{2}(1-\cos 2px)$ .
$\int \cos ax dx = \frac{1}{a} \sin ax + c$
$\spadesuit \, $ Menyederhanakan bentuk $\sin ^2 x \cos ^2 x$ :
$\begin{align*} \sin ^2 x \cos ^2 x & = (\sin x . \cos x)^2 \\ & = \left( \frac{1}{2}\sin 2x \right)^2 \\ & = \frac{1}{4} \sin ^2 2x \\ & = \frac{1}{4} \left[ \frac{1}{2}(1-\cos 4x) \right] \\ & = \frac{1}{8} (1-\cos 4x) \end{align*}$
$\spadesuit \, $ Menentukan hasil integral :
$\begin{align*} \int 8\sin ^2 x \cos ^2 x dx & = \int 8.\frac{1}{8} (1-\cos 4x) dx \\ & = \int (1 - \cos 4x )dx \\ & = x - \frac{1}{4}\sin 4x + c \end{align*}$
Jadi, hasil $\int 8\sin ^2 x \cos ^2 x dx = x - \frac{1}{4}\sin 4x + c. \heartsuit$
Nomor 9
Jika $L(a)$ adalah luas daerah yang dibatasi oleh sumbu X dan parabola $y=ax-x^2, \, 0 < a < 1,$
maka peluang nilai $a$ sehingga $L(a) \geq \frac{1}{12}$ adalah ...
$\clubsuit \, $ Pada kasus ini, tidak mungkin menghitung banyaknya nilai $a$ yang memenuhi (karena nilai $a$ ada tak hingga banyaknya), tetapi diwakili panjang garisnya.
$\clubsuit \, $ Nilai $a$ dipilih dari selang $0 < a < 1 $

sehingga panjang garisnya = 1 - 0 = 1. Diperoleh $n(S) = 1$
$\clubsuit \, $ Menghitung $L(a)$ :
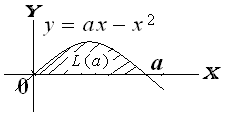
$\begin{align*} L(a) & =\int \limits_0^a (ax-x^2) dx = \left[ \frac{a}{2}x^2-\frac{1}{3}x^3 \right]_0^a = \frac{a}{2}.a^2-\frac{1}{3}a^3 = \frac{a^3}{6} \end{align*}$
$\clubsuit \, $ Menentukan batas $a$ dari $L(a) \geq \frac{1}{12}$ :
$\begin{align*} L(a) & \geq \frac{1}{12} \Leftrightarrow \frac{a^3}{6} \geq \frac{1}{12} \Leftrightarrow a^3 \geq \frac{1}{2} \Leftrightarrow a \geq \sqrt[3]{\frac{1}{2}} \Leftrightarrow a \geq \frac{1}{\sqrt[3]{2}} \end{align*}$

Panjang garis yang diinginkan = $1 - \frac{1}{\sqrt[3]{2}} $ . Diperoleh $n(A) = 1 - \frac{1}{\sqrt[3]{2}} $ .
Sehingga peluangnya : $P(A) = \frac{n(A)}{n(S)} = \frac{1 - \frac{1}{\sqrt[3]{2}}}{1}= 1 - \frac{1}{\sqrt[3]{2}} $ .
Jadi, peluangnya adalah $1 - \frac{1}{\sqrt[3]{2}} . \heartsuit $
$\clubsuit \, $ Nilai $a$ dipilih dari selang $0 < a < 1 $

sehingga panjang garisnya = 1 - 0 = 1. Diperoleh $n(S) = 1$
$\clubsuit \, $ Menghitung $L(a)$ :
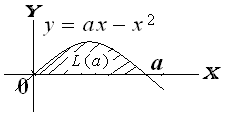
$\begin{align*} L(a) & =\int \limits_0^a (ax-x^2) dx = \left[ \frac{a}{2}x^2-\frac{1}{3}x^3 \right]_0^a = \frac{a}{2}.a^2-\frac{1}{3}a^3 = \frac{a^3}{6} \end{align*}$
$\clubsuit \, $ Menentukan batas $a$ dari $L(a) \geq \frac{1}{12}$ :
$\begin{align*} L(a) & \geq \frac{1}{12} \Leftrightarrow \frac{a^3}{6} \geq \frac{1}{12} \Leftrightarrow a^3 \geq \frac{1}{2} \Leftrightarrow a \geq \sqrt[3]{\frac{1}{2}} \Leftrightarrow a \geq \frac{1}{\sqrt[3]{2}} \end{align*}$

Panjang garis yang diinginkan = $1 - \frac{1}{\sqrt[3]{2}} $ . Diperoleh $n(A) = 1 - \frac{1}{\sqrt[3]{2}} $ .
Sehingga peluangnya : $P(A) = \frac{n(A)}{n(S)} = \frac{1 - \frac{1}{\sqrt[3]{2}}}{1}= 1 - \frac{1}{\sqrt[3]{2}} $ .
Jadi, peluangnya adalah $1 - \frac{1}{\sqrt[3]{2}} . \heartsuit $
Nomor 10
Luas daerah yang dibatasi oleh kurva $y=x^2-4$ dan $y=-3|x|$ adalah ...
$\spadesuit \, $ Menggambar grafik $y=x^2-4$ dan $y=-3|x|$
harga mutlak : $y=-3|x| = \left\{ \begin{array}{cc} -3x \, & , \text{untuk} \, x \geq 0 \\ -3(-x) = 3x \, & , \text{untuk} \, x < 0 \end{array} \right.$

$\spadesuit \, $ Dari gambar, luas daerah A sama dengan luas B,
sehingga Luas arsir = 2L$_A$ = 2L$_B$ .
$\spadesuit \, $ Menentukan Luas arsiran :
$\begin{align*} \text{Luas Arsir} &= 2\text{L}_A=2\int \limits_{-1}^0 (3x)-(x^2-4) dx = 2\int \limits_{-1}^0 (-x^2+3x+4)dx \\ & \text{Atau} \\ \text{Luas Arsir} &= 2\text{L}_B=2\int \limits_{0}^1 (-3x)-(x^2-4) dx = 2\int \limits_{0}^1 (-x^2-3x+4)dx \\ & \text{Atau} \\ \text{Luas Arsir} &= \text{L}_A + \text{L}_B=\int \limits_{-1}^0 (-x^2+3x+4)dx + \int \limits_{0}^1 (-x^2-3x+4)dx \end{align*}$
Jadi, Luasnya adalah $2\int \limits_{-1}^0 (-x^2+3x+4)dx \, $ atau $\, 2\int \limits_{0}^1 (-x^2-3x+4)dx \, $ atau $\, \int \limits_{-1}^0 (-x^2+3x+4)dx + \int \limits_{0}^1 (-x^2-3x+4)dx $ . Pilihlah salah satu yang ada di opsi. $\heartsuit $
harga mutlak : $y=-3|x| = \left\{ \begin{array}{cc} -3x \, & , \text{untuk} \, x \geq 0 \\ -3(-x) = 3x \, & , \text{untuk} \, x < 0 \end{array} \right.$

$\spadesuit \, $ Dari gambar, luas daerah A sama dengan luas B,
sehingga Luas arsir = 2L$_A$ = 2L$_B$ .
$\spadesuit \, $ Menentukan Luas arsiran :
$\begin{align*} \text{Luas Arsir} &= 2\text{L}_A=2\int \limits_{-1}^0 (3x)-(x^2-4) dx = 2\int \limits_{-1}^0 (-x^2+3x+4)dx \\ & \text{Atau} \\ \text{Luas Arsir} &= 2\text{L}_B=2\int \limits_{0}^1 (-3x)-(x^2-4) dx = 2\int \limits_{0}^1 (-x^2-3x+4)dx \\ & \text{Atau} \\ \text{Luas Arsir} &= \text{L}_A + \text{L}_B=\int \limits_{-1}^0 (-x^2+3x+4)dx + \int \limits_{0}^1 (-x^2-3x+4)dx \end{align*}$
Jadi, Luasnya adalah $2\int \limits_{-1}^0 (-x^2+3x+4)dx \, $ atau $\, 2\int \limits_{0}^1 (-x^2-3x+4)dx \, $ atau $\, \int \limits_{-1}^0 (-x^2+3x+4)dx + \int \limits_{0}^1 (-x^2-3x+4)dx $ . Pilihlah salah satu yang ada di opsi. $\heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.