Nomor 6
Jika $ \alpha \, $ dan $ \, \beta \, $ sudut lancip, $ \, \cos (\alpha - \beta ) = \frac{1}{2}\sqrt{3} \, $ dan
$ \cos \alpha \cos \beta = \frac{1}{2} , \, $ maka $ \, \frac{\cos (\alpha + \beta )}{\cos (\alpha - \beta )} = ..... $
$\spadesuit \, $ Konsep dasar
$ \cos (x-y) = \cos x \cos y + \sin x \sin y $
$ \cos (x+y) = \cos x \cos y - \sin x \sin y $
$\spadesuit \, $ Menentukan nilai $ \sin \alpha \sin \beta \, $
$\begin{align} \cos (\alpha - \beta ) & = \frac{1}{2}\sqrt{3} \\ \cos \alpha \cos \beta + \sin \alpha \sin \beta & = \frac{1}{2}\sqrt{3} \\ \frac{1}{2} + \sin \alpha \sin \beta & = \frac{1}{2}\sqrt{3} \\ \sin \alpha \sin \beta & = \frac{1}{2}\sqrt{3} - \frac{1}{2} \end{align}$
$\spadesuit \, $ Menentukan $ \, \cos (\alpha + \beta ) $
$\begin{align} \cos (\alpha + \beta ) & = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ \cos (\alpha + \beta ) & = \frac{1}{2} - ( \frac{1}{2}\sqrt{3} - \frac{1}{2} ) \\ \cos (\alpha + \beta ) & = 1 - \frac{1}{2}\sqrt{3} \end{align}$
$\spadesuit \, $ Menentukan hasilnya
$\begin{align} \frac{\cos (\alpha + \beta )}{\cos (\alpha - \beta )} & = \frac{1 - \frac{1}{2}\sqrt{3}}{\frac{1}{2}\sqrt{3}} \\ & = \frac{1 - \frac{1}{2}\sqrt{3}}{\frac{1}{2}\sqrt{3}} . \frac{2\sqrt{3}}{2\sqrt{3}} \\ & = \frac{2\sqrt{3} - 3}{3} \\ \frac{\cos (\alpha + \beta )}{\cos (\alpha - \beta )} & = \frac{2}{3}\sqrt{3} - 1 \end{align}$
Jadi, nilai $ \frac{\cos (\alpha + \beta )}{\cos (\alpha - \beta )} = \frac{2}{3}\sqrt{3} - 1 . \heartsuit $
$ \cos (x-y) = \cos x \cos y + \sin x \sin y $
$ \cos (x+y) = \cos x \cos y - \sin x \sin y $
$\spadesuit \, $ Menentukan nilai $ \sin \alpha \sin \beta \, $
$\begin{align} \cos (\alpha - \beta ) & = \frac{1}{2}\sqrt{3} \\ \cos \alpha \cos \beta + \sin \alpha \sin \beta & = \frac{1}{2}\sqrt{3} \\ \frac{1}{2} + \sin \alpha \sin \beta & = \frac{1}{2}\sqrt{3} \\ \sin \alpha \sin \beta & = \frac{1}{2}\sqrt{3} - \frac{1}{2} \end{align}$
$\spadesuit \, $ Menentukan $ \, \cos (\alpha + \beta ) $
$\begin{align} \cos (\alpha + \beta ) & = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ \cos (\alpha + \beta ) & = \frac{1}{2} - ( \frac{1}{2}\sqrt{3} - \frac{1}{2} ) \\ \cos (\alpha + \beta ) & = 1 - \frac{1}{2}\sqrt{3} \end{align}$
$\spadesuit \, $ Menentukan hasilnya
$\begin{align} \frac{\cos (\alpha + \beta )}{\cos (\alpha - \beta )} & = \frac{1 - \frac{1}{2}\sqrt{3}}{\frac{1}{2}\sqrt{3}} \\ & = \frac{1 - \frac{1}{2}\sqrt{3}}{\frac{1}{2}\sqrt{3}} . \frac{2\sqrt{3}}{2\sqrt{3}} \\ & = \frac{2\sqrt{3} - 3}{3} \\ \frac{\cos (\alpha + \beta )}{\cos (\alpha - \beta )} & = \frac{2}{3}\sqrt{3} - 1 \end{align}$
Jadi, nilai $ \frac{\cos (\alpha + \beta )}{\cos (\alpha - \beta )} = \frac{2}{3}\sqrt{3} - 1 . \heartsuit $
Nomor 7
Gradien garis singgung suatu kurva di titik ($x,y$) adalah $ 3\sqrt{x} $ . Jika kurva ini melalui titik (4,9),
maka persamaan garis singgung kurva ini di titik berabsis 1 adalah ....
$\clubsuit \, $ Konsep dasar
Gradien garis singgung : $ m = f^\prime (x) $
dan $ \, f(x) = \int f^\prime (x) \, dx $
integral : $ \int ax^n \, dx = \frac{a}{n+1} x^{n+1} + c $
$\clubsuit \, $ Menentukan fungsi $ f(x) \, $ dengan $ m = f^\prime (x) = 3\sqrt{x} \, $ dan substitusi titik (4,9)
$\begin{align} f(x) & = \int f^\prime (x) \, dx \\ f(x) & = \int 3\sqrt{x} \, dx = \int 3.x^\frac{1}{2} \, dx \\ f(x) & = 3.\frac{2}{3}.x^\frac{3}{2} + c \\ f(x) & = 2x\sqrt{x} + c \\ (4,9) \rightarrow f(x) & = 2x\sqrt{x} + c \\ 9 & = 2.4.\sqrt{4} + c \\ c & = -7 \end{align}$
Sehingga fungsinya : $ f(x) = 2x\sqrt{x} - 7 $
$\clubsuit \, $ Menentukan titik singgung di absis 1 ( $ x = 1 $ )
$\begin{align} x= 1 \rightarrow f(x) & = 2x\sqrt{x} - 7 \\ f(1) & = 2.1.\sqrt{1} - 7 = -5 \end{align}$
Sehingga titik singgungnya : ($x_1,y_1$) = (1,-5)
$\clubsuit \, $ Menentukan gradien garis singgung di absis 1 ( $ x = 1 $ )
$ x= 1 \rightarrow m = 3\sqrt{x} = 3\sqrt{1} = 3 $
$\clubsuit \, $ Menentukan persamaan garis singgung (PGS) di titik ($x_1,y_1$) = (1,-5) dan gradien $ m = 3 $
$\begin{align} y-y_1 & = m(x-x_1) \\ y-(-5) & = 3(x-1) \\ y+5 & = 3x - 3 \\ 3x - y - 8 & = 0 \end{align}$
Jadi, PGS nya adalah $ 3x - y - 8 = 0 . \heartsuit$
Gradien garis singgung : $ m = f^\prime (x) $
dan $ \, f(x) = \int f^\prime (x) \, dx $
integral : $ \int ax^n \, dx = \frac{a}{n+1} x^{n+1} + c $
$\clubsuit \, $ Menentukan fungsi $ f(x) \, $ dengan $ m = f^\prime (x) = 3\sqrt{x} \, $ dan substitusi titik (4,9)
$\begin{align} f(x) & = \int f^\prime (x) \, dx \\ f(x) & = \int 3\sqrt{x} \, dx = \int 3.x^\frac{1}{2} \, dx \\ f(x) & = 3.\frac{2}{3}.x^\frac{3}{2} + c \\ f(x) & = 2x\sqrt{x} + c \\ (4,9) \rightarrow f(x) & = 2x\sqrt{x} + c \\ 9 & = 2.4.\sqrt{4} + c \\ c & = -7 \end{align}$
Sehingga fungsinya : $ f(x) = 2x\sqrt{x} - 7 $
$\clubsuit \, $ Menentukan titik singgung di absis 1 ( $ x = 1 $ )
$\begin{align} x= 1 \rightarrow f(x) & = 2x\sqrt{x} - 7 \\ f(1) & = 2.1.\sqrt{1} - 7 = -5 \end{align}$
Sehingga titik singgungnya : ($x_1,y_1$) = (1,-5)
$\clubsuit \, $ Menentukan gradien garis singgung di absis 1 ( $ x = 1 $ )
$ x= 1 \rightarrow m = 3\sqrt{x} = 3\sqrt{1} = 3 $
$\clubsuit \, $ Menentukan persamaan garis singgung (PGS) di titik ($x_1,y_1$) = (1,-5) dan gradien $ m = 3 $
$\begin{align} y-y_1 & = m(x-x_1) \\ y-(-5) & = 3(x-1) \\ y+5 & = 3x - 3 \\ 3x - y - 8 & = 0 \end{align}$
Jadi, PGS nya adalah $ 3x - y - 8 = 0 . \heartsuit$
Nomor 8
Jumlah semua akar persamaan :
$ 10 (x^2-x-12)^{\log (x^2-x-12) } = (x-4)^2(x+3)^2 $
adalah .....
$ 10 (x^2-x-12)^{\log (x^2-x-12) } = (x-4)^2(x+3)^2 $
adalah .....
$\spadesuit \, $ Konsep logaritma
Sifat : $ {}^a \log b^n = n. {}^a \log b $
Definisi : $ {}^a \log x = c \leftrightarrow x = a^c $
$\spadesuit \, $ Misalkan : $ p = x^2 - x - 12 , \, $ dan $ \, a = \log p $
Manyelesaikan soalnya
$\begin{align} 10 (x^2-x-12)^{\log (x^2-x-12) } & = (x-4)^2(x+3)^2 \\ 10 (x^2-x-12)^{\log (x^2-x-12) } & = [(x-4)(x+3)]^2 \\ 10 (x^2-x-12)^{\log (x^2-x-12) } & = [x^2-x-12]^2 \\ 10 (p)^{\log (p) } & = p^2 \, \, \text{(log kan kedua ruas)} \\ \log ( 10 (p)^{\log (p) } ) & = \log ( p^2 ) \\ \log 10 + \log (p)^{\log p } & = 2 \log p \\ 1 + \log p . \log p & = 2 \log p \, \, \text{(subst. } \, a = \log p \, ) \\ 1 + a. a & = 2a \\ a^2 - 2a + 1 & = 0 \\ (a-1)(a-1) & = 0 \\ a_1 = 1 \vee a_2 & = 1 \\ a_1 = 1 \rightarrow \log p_1 & = 1 \rightarrow p_1 = 10^1 = 10 \\ a_2 = 1 \rightarrow \log p_2 & = 1 \rightarrow p_2 = 10^1 = 10 \end{align}$
$\spadesuit \, $ Menentukan jumlah akar-akarnya dengan $ p = x^2 - x - 12 $
$\begin{align} p_1 = 10 \rightarrow x^2 - x - 12 & = 10 \\ x^2 - x - 22 & = 0 \\ x_1 + x_2 = \frac{-b}{a} = \frac{-(-1)}{1} & = 1 \\ p_2 = 10 \rightarrow x^2 - x - 12 & = 10 \\ x^2 - x - 22 & = 0 \\ x_3 + x_4 = \frac{-b}{a} = \frac{-(-1)}{1} & = 1 \end{align}$
Sehingga jumlah semua akar-akarnya :
$ x_1 + x_2 + x_3 + x_4 = 1 + 1 = 2 $
Jadi, jumlah semua akar-akarnya adalah 2. $ \heartsuit$
Sifat : $ {}^a \log b^n = n. {}^a \log b $
Definisi : $ {}^a \log x = c \leftrightarrow x = a^c $
$\spadesuit \, $ Misalkan : $ p = x^2 - x - 12 , \, $ dan $ \, a = \log p $
Manyelesaikan soalnya
$\begin{align} 10 (x^2-x-12)^{\log (x^2-x-12) } & = (x-4)^2(x+3)^2 \\ 10 (x^2-x-12)^{\log (x^2-x-12) } & = [(x-4)(x+3)]^2 \\ 10 (x^2-x-12)^{\log (x^2-x-12) } & = [x^2-x-12]^2 \\ 10 (p)^{\log (p) } & = p^2 \, \, \text{(log kan kedua ruas)} \\ \log ( 10 (p)^{\log (p) } ) & = \log ( p^2 ) \\ \log 10 + \log (p)^{\log p } & = 2 \log p \\ 1 + \log p . \log p & = 2 \log p \, \, \text{(subst. } \, a = \log p \, ) \\ 1 + a. a & = 2a \\ a^2 - 2a + 1 & = 0 \\ (a-1)(a-1) & = 0 \\ a_1 = 1 \vee a_2 & = 1 \\ a_1 = 1 \rightarrow \log p_1 & = 1 \rightarrow p_1 = 10^1 = 10 \\ a_2 = 1 \rightarrow \log p_2 & = 1 \rightarrow p_2 = 10^1 = 10 \end{align}$
$\spadesuit \, $ Menentukan jumlah akar-akarnya dengan $ p = x^2 - x - 12 $
$\begin{align} p_1 = 10 \rightarrow x^2 - x - 12 & = 10 \\ x^2 - x - 22 & = 0 \\ x_1 + x_2 = \frac{-b}{a} = \frac{-(-1)}{1} & = 1 \\ p_2 = 10 \rightarrow x^2 - x - 12 & = 10 \\ x^2 - x - 22 & = 0 \\ x_3 + x_4 = \frac{-b}{a} = \frac{-(-1)}{1} & = 1 \end{align}$
Sehingga jumlah semua akar-akarnya :
$ x_1 + x_2 + x_3 + x_4 = 1 + 1 = 2 $
Jadi, jumlah semua akar-akarnya adalah 2. $ \heartsuit$
Nomor 9
Luas sebuah lingkaran adalah fungsi dari kelilingnya. Jika keliling sebuah lingkaran adalah $ x $ , maka laju perubahan
luas lingkaran terhadap kelilingnya adalah ....
$\clubsuit \, $ Menentukan luas lingkaran dalam $ x $
$\begin{align} \text{ Keliling lingkaran } \, & = 2\pi r \\ x & = 2\pi r \\ r & = \frac{x}{2\pi} \\ \text{Luas Lingkaran } \, & = \pi r^2 \\ & = \pi \left( \frac{x}{2\pi} \right)^2 \\ L & = \frac{x^2}{4\pi } \end{align}$
$\clubsuit \, $ Laju luas adalah turunan
$\begin{align} \text{ Laju Luas } \, & = L^\prime \\ & = \frac{2x}{4\pi} \\ & = \frac{x}{2\pi} \end{align}$
Jadi, laju perubahan luasnya adalah $ \frac{x}{2\pi} . \heartsuit $
$\begin{align} \text{ Keliling lingkaran } \, & = 2\pi r \\ x & = 2\pi r \\ r & = \frac{x}{2\pi} \\ \text{Luas Lingkaran } \, & = \pi r^2 \\ & = \pi \left( \frac{x}{2\pi} \right)^2 \\ L & = \frac{x^2}{4\pi } \end{align}$
$\clubsuit \, $ Laju luas adalah turunan
$\begin{align} \text{ Laju Luas } \, & = L^\prime \\ & = \frac{2x}{4\pi} \\ & = \frac{x}{2\pi} \end{align}$
Jadi, laju perubahan luasnya adalah $ \frac{x}{2\pi} . \heartsuit $
Nomor 10
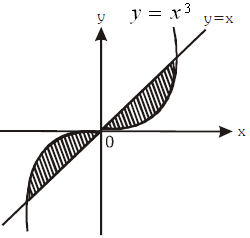
Daerah yang diarsir dapat dinyatakan sebagai himpunan titik ....

Daerah yang diarsir dapat dinyatakan sebagai himpunan titik ....
$\spadesuit \, $ Menganalisa setiap daerah di kuadran I dan III
$\spadesuit \, $ Daerah arsiran Kuadran I
Garis :
yang diarsir di bawah garis, sehingga $ y \leq x \, $ atau $ |y| \leq |x| $
Kurva :
yang diarsir di atas kurva, sehingga $ y \geq x^3 \, $ atau $ |y| \geq |x^3| $
Dari kuadran I ini, diperoleh $ |x^3| \leq |y| \leq |x| \, $ ....(i)
$\spadesuit \, $ Daerah arsiran Kuadran III
Garis :
yang diarsir di atas garis, sehingga $ y \geq x $ .
Karena Kuadran III nilai $ x $ dan $ y $ negatif, maka ketika diberi nilai mutlak, tanda ketaksamaan di balik
( contoh : $ -2 \geq -5 , \, $ maka $ |-2|=2 \leq |-5| =5 $ ).
Sehingga, $ y \geq x \, $ atau $ \, |y| \leq | x| $
Kurva :
yang diarsir di bawah kurva, sehingga $ y \leq x^3 \, $ atau $ |y| \geq |x^3| $
Dari kuadran III ini, diperoleh $ |x^3| \leq |y| \leq |x| \, $ ....(ii)
Jadi, dari dua daerah arsiran baik di kuadran I maupun kuadran III (bentuk (i) dan bentuk (ii) ) diperoleh hasil yang sama yaitu $ |x^3| \leq |y| \leq |x| . \heartsuit $
$\spadesuit \, $ Daerah arsiran Kuadran I
Garis :
yang diarsir di bawah garis, sehingga $ y \leq x \, $ atau $ |y| \leq |x| $
Kurva :
yang diarsir di atas kurva, sehingga $ y \geq x^3 \, $ atau $ |y| \geq |x^3| $
Dari kuadran I ini, diperoleh $ |x^3| \leq |y| \leq |x| \, $ ....(i)
$\spadesuit \, $ Daerah arsiran Kuadran III
Garis :
yang diarsir di atas garis, sehingga $ y \geq x $ .
Karena Kuadran III nilai $ x $ dan $ y $ negatif, maka ketika diberi nilai mutlak, tanda ketaksamaan di balik
( contoh : $ -2 \geq -5 , \, $ maka $ |-2|=2 \leq |-5| =5 $ ).
Sehingga, $ y \geq x \, $ atau $ \, |y| \leq | x| $
Kurva :
yang diarsir di bawah kurva, sehingga $ y \leq x^3 \, $ atau $ |y| \geq |x^3| $
Dari kuadran III ini, diperoleh $ |x^3| \leq |y| \leq |x| \, $ ....(ii)
Jadi, dari dua daerah arsiran baik di kuadran I maupun kuadran III (bentuk (i) dan bentuk (ii) ) diperoleh hasil yang sama yaitu $ |x^3| \leq |y| \leq |x| . \heartsuit $
Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.