Nomor 1
Jika x dan y memenuhi pertaksamaan y2−2<x dan persamaan 2y−x+1=0 , maka
x+y memenuhi pertaksamaan ....
♣ Substitusi pers(i) ke perts(ii)
2y−x+1=0→x=2y+1 ....pers(i)
y2−2<x→y2−2−x<0
perts(ii) : y2−2−x<0y2−2−(2y+1)<0y2−2y−3<0(y+1)(y−3)<0y=−1∨y=3

sehingga nilai y : −1<y<3
♣ Substitusi nilai y ke pers(i)
y=3→x=2y+1=2.3+1=7
y=−1→x=2y+1=2.(−1)+1=−1
sehingga nilai x : −1<x<7
Jumlah nilai x dan y , diperoleh :
−1<y<3−1<x<7+−2<x+y<10
Jadi, diperoleh −2<x+y<10.♡
2y−x+1=0→x=2y+1 ....pers(i)
y2−2<x→y2−2−x<0
perts(ii) : y2−2−x<0y2−2−(2y+1)<0y2−2y−3<0(y+1)(y−3)<0y=−1∨y=3

sehingga nilai y : −1<y<3
♣ Substitusi nilai y ke pers(i)
y=3→x=2y+1=2.3+1=7
y=−1→x=2y+1=2.(−1)+1=−1
sehingga nilai x : −1<x<7
Jumlah nilai x dan y , diperoleh :
−1<y<3−1<x<7+−2<x+y<10
Jadi, diperoleh −2<x+y<10.♡
Nomor 2
Jika salah satu akar persamaan x6−kx=12 adalah -6, maka akar yang lain adalah ....
♠ Menyederhanakan soal
x6−kx=12 ( kali 6x)x2−6k=3xx2−3x−6k=0a=1,b=−3,c=−6k
♠ Salah satu akarnya -6 , artinya x1=−6
♠ Menentukan nilai k dengan substitusi x1=−6
x1=−6→x2−3x−6k=0(−6)2−3.(−6)−6k=036+18−6k=0k=9
PK : x2−3x−6.9=0→x2−3x−54=0
♠ Menentukan akar-akar dengan pemfaktoran
x2−3x−54=0(x+6)(x−9)=0x=−6∨x=9
Jadi, akar yang lainnya adalah 9. ♡
x6−kx=12 ( kali 6x)x2−6k=3xx2−3x−6k=0a=1,b=−3,c=−6k
♠ Salah satu akarnya -6 , artinya x1=−6
♠ Menentukan nilai k dengan substitusi x1=−6
x1=−6→x2−3x−6k=0(−6)2−3.(−6)−6k=036+18−6k=0k=9
PK : x2−3x−6.9=0→x2−3x−54=0
♠ Menentukan akar-akar dengan pemfaktoran
x2−3x−54=0(x+6)(x−9)=0x=−6∨x=9
Jadi, akar yang lainnya adalah 9. ♡
Cara II
♠ Menyederhanakan soal
x6−kx=12 ( kali 6x)x2−6k=3xx2−3x−6k=0a=1,b=−3,c=−6k
♠ Salah satu akarnya -6 , artinya x1=−6
♠ Menentukan x2 dari operasi akar
x1+x2=−ba−6+x2=−(−3)1−6+x2=3x2=9
Jadi, akar yang lainnya adalah 9. ♡
Catatan : Pada pembahasan ini tidak perlu menentukan nilai k dulu
♠ Menyederhanakan soal
x6−kx=12 ( kali 6x)x2−6k=3xx2−3x−6k=0a=1,b=−3,c=−6k
♠ Salah satu akarnya -6 , artinya x1=−6
♠ Menentukan x2 dari operasi akar
x1+x2=−ba−6+x2=−(−3)1−6+x2=3x2=9
Jadi, akar yang lainnya adalah 9. ♡
Catatan : Pada pembahasan ini tidak perlu menentukan nilai k dulu
Nomor 3
3∫−3|x2−2x−3|dx=....
♣ Menentukan interval positif dan negatif fungsi
x2−2x−3=0(x+1)(x−3)=0x=−1∨x=3
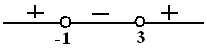
Artinya fungsi f(x)=x2−2x−3 bernilai negatif saat −1≤x≤3 dan selain itu positif.
♣ Definisi harga mutlak
|f(x)|={f(x),untuk f(x)≥0(positif)−f(x),untuk f(x)<0(negatif)
Sehingga untuk f(x)=x2−2x−3
|x2−2x−3|={x2−2x−3,x≤−1∨x≥3−(x2−2x−3),−1<x<3
Artinya :
Untuk x≤−1∨x≥3→|x2−2x−3|=x2−2x−3
Untuk −1<x<3
→|x2−2x−3|=−(x2−2x−3)=−x2+2x+3
♣ Sifat integral : c∫af(x)dx=b∫af(x)dx+c∫bf(x)dx
♣ Menyelesaikan integral dengan sifat dan harga mutlak
3∫−3|x2−2x−3|dx=−1∫−3|x2−2x−3|dx+3∫−1|x2−2x−3|dx=−1∫−3(x2−2x−3)dx+3∫−1(−x2+2x+3)dx=(13x3−x2−3x)−1−3+(−13x3+x2+3x)3−1=323+323=643
Jadi, hasil integralnya adalah 643.♡
Catatan : Soal ini sulit karena melibatkan harga mutlak dan batasnya harus dipecah.
x2−2x−3=0(x+1)(x−3)=0x=−1∨x=3
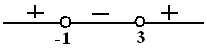
Artinya fungsi f(x)=x2−2x−3 bernilai negatif saat −1≤x≤3 dan selain itu positif.
♣ Definisi harga mutlak
|f(x)|={f(x),untuk f(x)≥0(positif)−f(x),untuk f(x)<0(negatif)
Sehingga untuk f(x)=x2−2x−3
|x2−2x−3|={x2−2x−3,x≤−1∨x≥3−(x2−2x−3),−1<x<3
Artinya :
Untuk x≤−1∨x≥3→|x2−2x−3|=x2−2x−3
Untuk −1<x<3
→|x2−2x−3|=−(x2−2x−3)=−x2+2x+3
♣ Sifat integral : c∫af(x)dx=b∫af(x)dx+c∫bf(x)dx
♣ Menyelesaikan integral dengan sifat dan harga mutlak
3∫−3|x2−2x−3|dx=−1∫−3|x2−2x−3|dx+3∫−1|x2−2x−3|dx=−1∫−3(x2−2x−3)dx+3∫−1(−x2+2x+3)dx=(13x3−x2−3x)−1−3+(−13x3+x2+3x)3−1=323+323=643
Jadi, hasil integralnya adalah 643.♡
Catatan : Soal ini sulit karena melibatkan harga mutlak dan batasnya harus dipecah.
Nomor 4
Diketahui kubus ABCD.EFGH dengan panjang rusuk a . P dan Q masing - masing merupakan titik tengah AB dan CD,
sedangkan R merupakan titik perpotongan EG dan FH. Jarak titik R ke bidang EPQH adalah ....
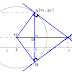
♠ Gambar

Jarak R ke bidang EPQH = panjang RO ( jarak terdekatnya)
NR=12NK=12a
MN=√MR2+RN2=√a2+(12a)2=12a√5
♠ Menentukan panjang RO dengan luas segitiga MNR
LΔMNR(alas MR)=LΔMNR(alas MN)12.MR.RN=12.MN.ROMR.RN=MN.ROa.12a=12a√5.ROa=√5.RORO=a√5=a5√5
Jadi, jaraknya adalah a5√5.♡

Jarak R ke bidang EPQH = panjang RO ( jarak terdekatnya)
NR=12NK=12a
MN=√MR2+RN2=√a2+(12a)2=12a√5
♠ Menentukan panjang RO dengan luas segitiga MNR
LΔMNR(alas MR)=LΔMNR(alas MN)12.MR.RN=12.MN.ROMR.RN=MN.ROa.12a=12a√5.ROa=√5.RORO=a√5=a5√5
Jadi, jaraknya adalah a5√5.♡
Nomor 5
Diketahui suatu persamaan parabola y=ax2+bx+c. Jika a,b dan c berturut - turut merupakan
suku pertama, kedua, dan ketiga suatu barisan aritmetika, serta garis singgung parabola tersebut di titik (1,12) sejajar
dengan garis y=6x , maka nilai (3a+2b+c)=....
♣ Barisan aritmatika : a,b,c
Selisih sama : b−a=c−b→a+c=2b ....pers(i)
♣ Substitusi titik (1,12) ke parabola
(1,12)→y=ax2+bx+c12=a.12+b.1+ca+b+c=12...pers(ii)
♣ Substitusi pers(i) ke pers(ii)
a+b+c=12(a+c)+b=122b+b=12→b=4
♣ Gradien garis : y=6x→m1=6
Karena sejajar, maka gradien garis singgungnya sama dengan gradien garis y=6x , sehingga m=6
♣ Gradien garis singgung : m=f′(x)
y=ax2+bx+c→y′=2ax+bm=f′(1)6=2a.1+b2a+b=6b=4→2a+4=62a=2→a=1
pers(i) : a+c=2b→1+c=2.4→c=7
Sehingga nilai 3a+2b+c=3.1+2.4+7=3+8+7=18
Jadi, nilai 3a+2b+c=18.♡
Selisih sama : b−a=c−b→a+c=2b ....pers(i)
♣ Substitusi titik (1,12) ke parabola
(1,12)→y=ax2+bx+c12=a.12+b.1+ca+b+c=12...pers(ii)
♣ Substitusi pers(i) ke pers(ii)
a+b+c=12(a+c)+b=122b+b=12→b=4
♣ Gradien garis : y=6x→m1=6
Karena sejajar, maka gradien garis singgungnya sama dengan gradien garis y=6x , sehingga m=6
♣ Gradien garis singgung : m=f′(x)
y=ax2+bx+c→y′=2ax+bm=f′(1)6=2a.1+b2a+b=6b=4→2a+4=62a=2→a=1
pers(i) : a+c=2b→1+c=2.4→c=7
Sehingga nilai 3a+2b+c=3.1+2.4+7=3+8+7=18
Jadi, nilai 3a+2b+c=18.♡








Admin, nomer 3 dibagian definisi nilai mutlaknya ada yang ketuker ya ?
BalasHapusHallow @Reihan A,
HapusTerimakasih untuk koreksinya demi perbaikan isi artikel pada blog dunia-informa ini.
Iya, untuk bentuk mutlaknya terbalik, dan sudah kami perbaiki.
Terimakasih untuk kunjungannya ke blog ini.
Tetap semangat belajarnya.